Table of Contents

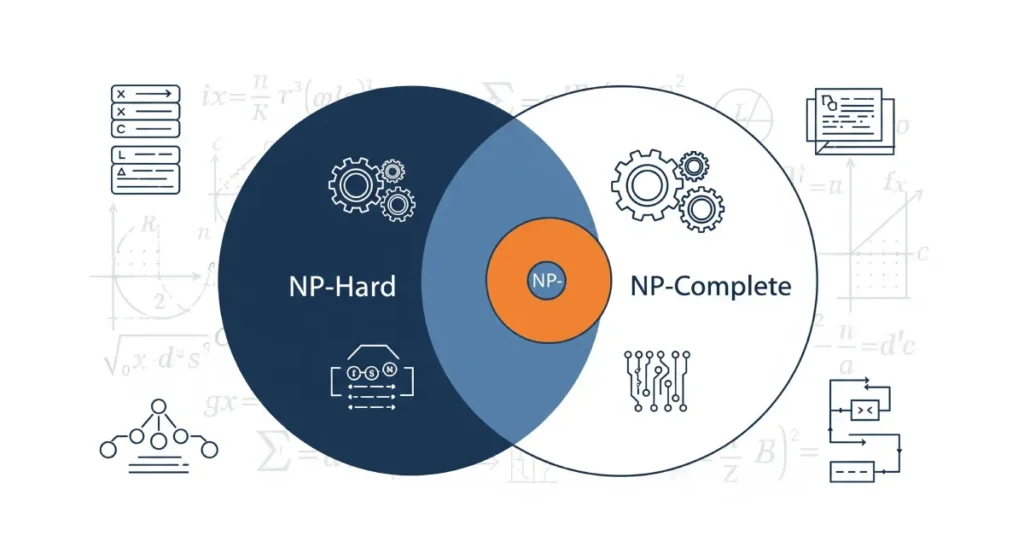
Key Differences: NP-Hard vs NP-Complete
NP-Hard | NP-Complete |
|---|---|
| NP-hard is the class of decision problems to which all problems in NP can be reduced to in polynomial time by a deterministic Turing machine. | NP-complete is the class of decision problems in NP to which all problems in NP can be reduced to in polynomial time by a deterministic Turing machine. |
| NP-hard ⊄ NP or NP ⊄ NP-hard. | NP-complete ⊂ NP. |
| Not all NP-hard problems are NP-complete. For an NP-hard problem to be NP-complete, it must be in NP. | All NP-complete problems are NP-hard |
| If any problem in NP can be reduced to it in polynomial time. | If any problem in NP can be reduced to it in polynomial time AND it is also in NP (and thus solutions can be verified in polynomial time). |
| These are the problems that are at least as hard as the NP-complete problems. Note that NP-hard problems do not have to be in NP, and they do not have to be decision problems. | NP-Complete is a complexity class which represents the set of all problems in NP for which it is possible to reduce any other NP problem in polynomial time. |
Understanding NP-Hard Problems
NP-Hard problems rank among the most challenging computational problems we face. What defines them is a simple yet powerful characteristic: they are at least as difficult as the hardest problems in the NP complexity class.
Key Characteristics of NP-Hard Problems:
- Reduction Property: We can reduce every problem in NP to an NP-Hard problem in polynomial time.
- Not Necessarily in NP: Unlike NP-Complete problems, NP-Hard problems don’t need to belong to the NP class
- Solution Verification: There’s no requirement that solutions can be verified quickly
- Problem Type: Can include optimization problems, not just decision problems
This flexibility makes NP-Hard a broader category that encompasses problems that might be even harder than those in NP.
Understanding NP-Complete Problems
NP-Complete problems occupy a special position in computational complexity theory. They represent the “hardest” problems within the NP class, meaning they are both in NP and as difficult as any problem in NP.
Key Characteristics of NP-Complete Problems:
- Membership in NP: Solutions can be verified in polynomial time
- Universal Reducibility: Every problem in NP can be transformed into an NP-Complete problem using a polynomial-time reduction.
- Decision Problems: Typically framed as yes/no questions
- Interconnected Nature: If one NP-Complete problem can be solved in polynomial time, all can be
This interconnectedness makes NP-Complete problems central to the famous P vs NP question in computer science.
Real-World Examples
Common NP-Complete Problems:
- Traveling Salesman Problem (TSP): Finding the shortest route visiting all cities exactly once
- Boolean Satisfiability (SAT): Determines whether a Boolean formula has at least one assignment of truth values that makes the formula true.
- Knapsack Problem: Selecting items with maximum value within weight constraints
- Graph Coloring: Assigning colors to graph vertices with no adjacent vertices sharing colors
Examples of NP-Hard Problems:
- Optimization versions of NP-Complete problems: Finding the actual shortest TSP route (not just determining if one exists)
- Chess and Go: Determining optimal play from any position
- Halting Problem: Determining if a program will halt on a given input
These examples show how NP-Hard and NP-Complete problems appear in practical applications, from logistics and scheduling to game theory and program analysis.
Frequently Asked Questions
What does NP-Complete mean?
NP-Complete problems are those that are both in NP and as hard as any problem in NP. If you can solve an NP-Complete problem in polynomial time, you can solve all NP problems in polynomial time. This makes them the “hardest” problems within the NP complexity class.
What does NP-Hard mean?
NP-Hard problems are at least as hard as the hardest problems in NP, but they may not be in NP themselves. An NP-Hard problem doesn’t necessarily have to be solvable in polynomial time, nor does it need to be verifiable in polynomial time. This makes NP-Hard a broader category than NP-Complete.
Is every NP-Complete problem NP-Hard?
Yes, every NP-Complete problem is NP-Hard because it is as hard as any problem in NP. However, not all NP-Hard problems are NP-Complete, because they may not be in NP. Think of NP-Complete as a subset of NP-Hard problems.
Can an NP-Complete problem be solved in polynomial time?
Currently, no one has proven that any NP-Complete problem can be solved in polynomial time. Proving this would mean that P = NP—one of the most important and unresolved questions in computer science and mathematics.
Why should I care about NP-Hard vs NP-Complete?
Understanding these concepts helps you recognize when you’re dealing with inherently difficult problems. This knowledge guides you toward appropriate solution strategies, such as approximation algorithms, heuristics, or accepting exponential-time solutions for small inputs.
Are there practical algorithms for NP-Hard and NP-Complete problems?
Although researchers haven’t discovered any polynomial-time algorithms for these problems, they have developed several practical approaches: approximation algorithms that deliver near-optimal solutions, heuristic methods that perform well in practice, and exact algorithms that efficiently handle small problem instances.
Conclusion
Understanding the distinction between NP-Hard vs NP-Complete is crucial for grasping the complexity of computational problems. NP-Complete problems are the hardest problems within NP, while NP-Hard problems may not even belong to NP but are still at least as difficult to solve as the hardest NP problems.
While computer scientists often debate whether they can solve NP problems in polynomial time, the concepts of NP-Complete and NP-Hard help them categorize the difficulty of various computational tasks. This understanding enables developers and researchers to choose appropriate problem-solving strategies and set realistic expectations for algorithm performance.
Whether you’re optimizing delivery routes, scheduling resources, or analyzing complex systems, recognizing these problem types will guide you toward the most effective approaches for your specific computational challenges.