Difference Between Prim’s and Kruskal’s Algorithm

Understanding the difference between Prim’s and Kruskal’s algorithm is essential in graph theory. Prim’s algorithm grows a minimum spanning tree by starting from a single vertex and expanding, while Kruskal’s algorithm sorts edges and selects the smallest ones to form the tree. This guide highlights their processes, advantages, and applications./p>

 

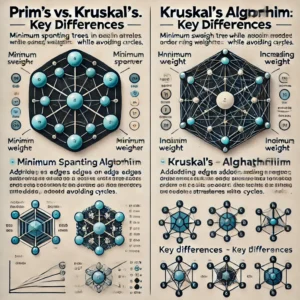
Key Differences Between Prim’s and Kruskal’s Algorithm

 

Prim’s Algorithm	Kruskal’s Algorithm
It begins with a Node.	It begins with an edge.
It starts to build the MST Set from any of the Nodes.	It starts to build the MST Set from minimum weighted vertex in the graph.
Run Faster in dense graphs.	Run faster in sparse graphs.
The graph must be a connected graph.	It works on the connected and disconnected graph.
Traverse the one node several times to get the minimum distance.	Traverse the edge only once.
Time Complexity is O(E*V logV) with binary heap and O(E+V logV) with the Fibonacci heap.	Time Complexity is O(E logV)
Binary or Fibonacci Heap, Adjencacy Matrix are used.	Disjoint Set is used.
The next node included must be connected with the node we traverse.	The next edge includes may or may not be connected but should not form a cycle.
Doesn’t check cycle is formed or not.	The check cycle is formed or not. If formed then discard the nodes.

 

FAQs

1. What is Prim’s Algorithm?

It is a greedy approach that helps find the minimum spanning tree (MST) of a connected, undirected graph. It starts with a single vertex and expands the MST by adding the smallest edge that connects a vertex in the tree to a vertex outside the tree, avoiding the formation of cycles.

2. What is Kruskal’s Algorithm?

It follows a greedy approach to find the MST of a graph. It processes all edges and adds the smallest one that does not form a cycle. This process continues until the algorithm connects all vertices.

3. How do the approaches of Prim’s and Kruskal’s algorithms differ?

Prim’s Algorithm grows the MST one vertex at a time, starting with an arbitrary vertex. It adds the smallest edge that connects a new vertex to the tree. Kruskal’s Algorithm, however, processes edges by weight and adds the smallest edge without forming a cycle, regardless of the vertices it connects.

4. Which algorithm is more efficient in sparse graphs, Prim’s or Kruskal’s?

The Kruskal’s Algorithm tends to be more efficient in sparse graphs because it processes edges directly without checking all vertices. It works well when the graph has fewer edges. Prim’s algorithm, however, may be slower in sparse graphs since it depends on a priority queue to find the minimum edge connecting to the tree.

5. In what situations is Prim’s Algorithm preferred over Kruskal’s Algorithm?

People prefer Prim’s Algorithm for dense graphs with many edges. It efficiently adds vertices one by one, making it ideal when the graph has a high edge-to-vertex ratio.

Conclusion

In conclusion, both Prim’s and Kruskal’s algorithms efficiently find the minimum spanning tree in a graph, but they differ in their approach. Prim’s algorithm is ideal for dense graphs and expands the tree one vertex at a time, while Kruskal’s algorithm suits sparse graphs by focusing on sorting edges and avoiding cycles. Choosing between the two algorithms depends on the graph’s structure and the problem’s specific requirements.